Definícia:
Chí-kvadrát (χ2) test nezávislosti, známy tiež ako Pearsonov χ2 test alebo χ2 test asociácie, je možné použiť na zistenie asociácie medzi nominálnymi premennými. Test pracuje s kontingenčnou (krížovou) tabuľkou, ktorá zobrazuje počty hodnôt premennej v jednotlivých kategóriách. Test overuje nulovú hypotézu, že medzi dvoma nominálnymi premennými neexistuje žiadna súvislosť, pričom porovnáva pozorované/zistené/namerané (Observed) počty s očakávanými (Expected), ktoré dostaneme vtedy, ak medzi premennými neexistuje žiadna súvislosť (JASP, n.d.).
Predpoklady pre použitie Chí-kvadrát (χ2) testu nezávislosti podľa JASP, n.d. a SPSS Statistics Tutorials and Statistical Guides | Laerd Statistics, n.d.:
- Premenné musia byť nominálne alebo ordinálne. V prípade, že bude premenná ordinálna, test s ňou bude pracovať ako s nominálnom a poradie hodnôt nebude zohrávať žiadnu rolu.
- Premenné musia obsahovať dve, či viac kategórií, teda musia byť minimálne binárne.
- Vo všetkých bunkách kontingenčnej tabuľky by mali byť očakávané početnosti vyššie ako 5.
Koeficient phi je štatistická metóda, ktorou vieme merať vzťah medzi dvoma dichotomickými premennými. Napríklad pohlavie (muž – žena) a typ športovej aktivity (kolektívny – individuálny). Výsledok nadobúda hodnoty v intervale 0 až 1, kde 0 znamená žiadny vzťah a 1 úplný vzťah (Hanák, 2016). Koeficient phi je vhodné počítať iba vtedy, keď máte dve dichotomické premenné.
Cramerovo V meria vzájomný vzťah medzi dvoma premennými, z ktorých jedna či obe majú vyšší počet kategórií ako dve – teda polynomické premenné. Podobne ako koeficient phi nadobúda hodnotu od 0 do 1, kde 0 znamená žiadny vzťah a 1 úplný vzťah (Rabušic et al., 2019).
Príklad:
Pod týmto textom uvádzam príklad použitia Chí-kvadrát (χ2) test nezávislosti, koeficientu phi a Cramerovho V. Dátový súbor obsahuje tri premenné: pohlavie = muži a ženy; sport_typ = kolektívny a individuálny a sport_intenzita = nízka, stredná, vysoká. Chceme zistiť, či existuje asociácia medzi pohlavím a typom športu a tiež či exituje asociácia medzi pohlavím a intenzitou športu. Ak by sme z vyššie uvedeného formulovali výskumné otázky, zneli by nasledovne:
VO1: Existuje asociácia medzi pohlavím a typom športovej aktivity – individuálnej, či kolektívnej?
VO2: Existuje asociácia medzi pohlavím a intenzitou športovej aktivity – nízkou, strednou, vysokou?
Dátový súbor si môžete stiahnuť tu.
Postup:
Z nižšie uvedených možností v menu budeme pracovať s „Descriptives“, tým získame základné údaje popisnej štatistiky a „Frequencies“, kde zvolíme „Contingency Tables“, čím získame kontingenčnú (krížovú) tabuľku.

Vo voľbách popisnej štatistiky „Descriptive Statistics“ presunieme premennú sport_typ a sport_intenzita do okna „Variables“ a premennú pohlavie do okna „Split“, ako je to zobrazené nižšie.
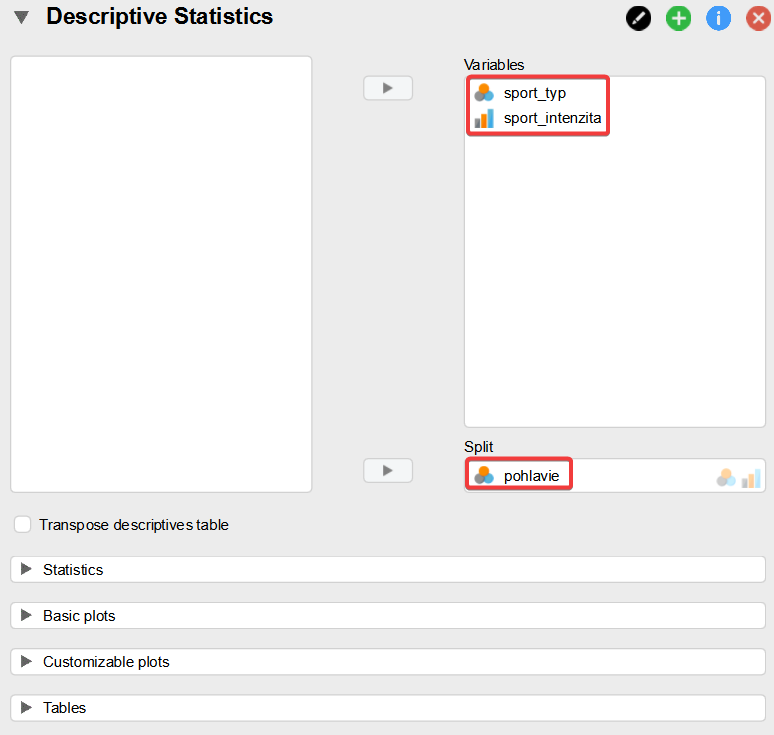
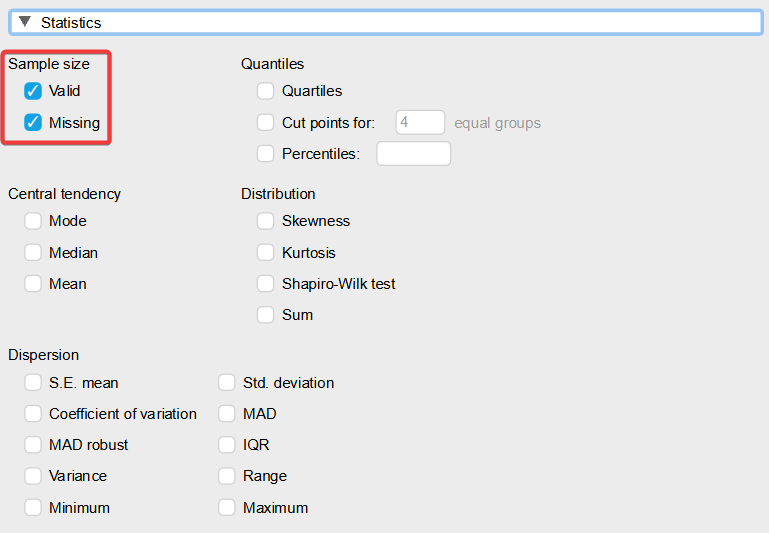
V časti „Statistics“ úplne stačí zvoliť „Valid“ a „Missing“, čím dostaneme informácie o počte platných a chýbajúcich hodnotách v dátovom súbore. Zvyšné položky nemá zmysel zvoliť, keďže pracujeme s nominálnymi premennými.
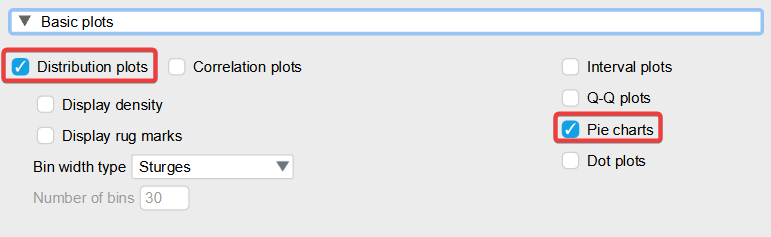
Presunieme sa do časti „Basic plots“. Tu zvolíme „Distribution plots“, čím získame stĺpcové grafy porovnania pohlaví v športových aktivitách. Ak zvolíme možnosť „Pie charts“, získame koláčové grafy, viď nižšie.
V časti „Tables“ zvolíme možnosť „Frekvency tables“, čo nám vo výstupe poskytne údaje o počtoch – frekvencii pohlaví a športov.

Vo voľbách kontingenčnej tabuľky „Contingency Tables“ presunieme premennú sport_typ do okna „Columns“ a premennú pohlavie do okna „Rows“, ako je to zobrazené nižšie. Tak vypočítame štatistiky pre VO1.
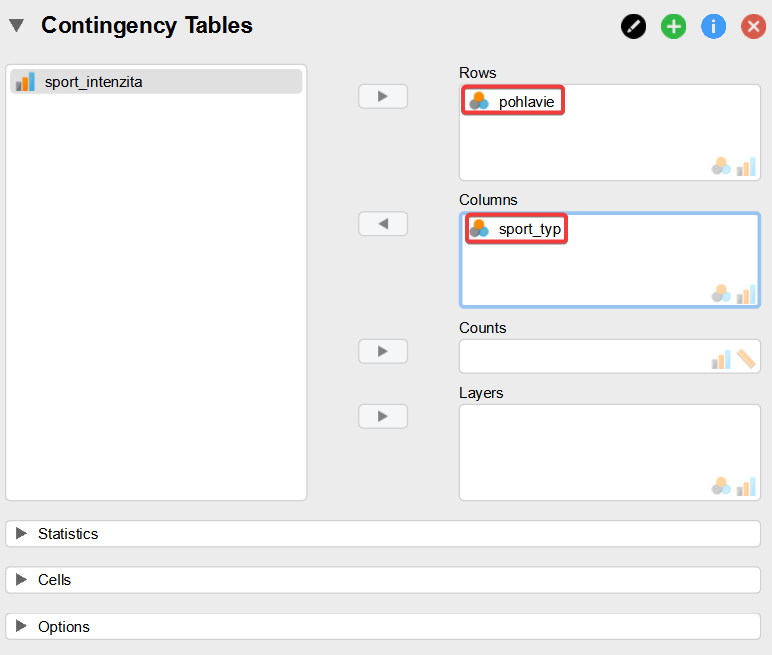
Ďalej otvoríme časť „Statistics“ a zvolíme „χ2“ = Chí-kvadrát (χ2) test nezávislosti a „Phi and Cramer´s V“.
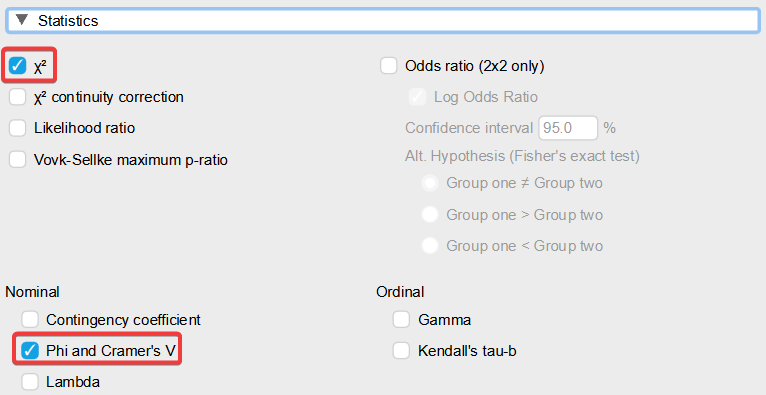
V časti „Cells“ zvolíme „Expected“ – to nám zobrazí očakávané početnosti. Budeme teda vo výsledku vidieť, aký je rozdiel medzi zistenými početnosťami (Count) a očakávanými početnosťami (Expected). Môžeme zvoliť aj zobrazenie percent pod „Percentages“. „Row“ pre riadkové percentá a „Column“ pre stĺpcové percentá kontingenčnej tabuľky.
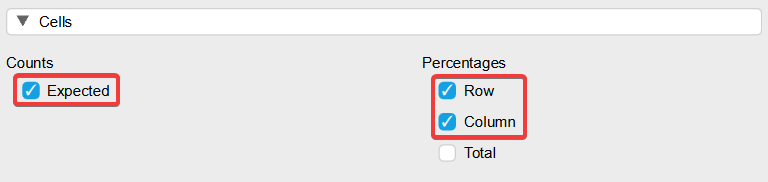
Tak ako sme na začiatku analýzy zvolili „Frekvencies“ a následne „Contingency Tables“, teraz to urobíme znova, pretože chceme zodpovedať na VO2, kde skúmame asociáciu medzi pohlavím a intenzitou športovej aktivity.

V novo vytvorenej časti „Contingency Tables“ presunieme do okna „Rows“ premennú pohlavie a do okna „Columns“ premennú sport_intenzita.
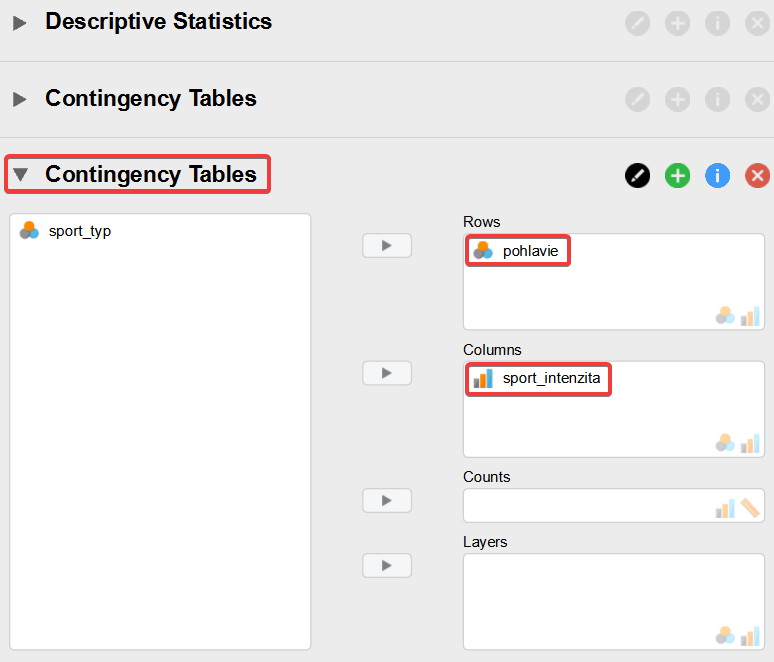
Podobne, ako sme to robili pri zadávaní analýzy pre VO1, zvolíme možnosti aj pre VO2. Teda v časti „Statistics“ zvolíme „χ2“ a „Phi and Cramer´s V“.

V časti „Cells“ zvolíme „Expected“ – to nám zobrazí očakávané početnosti. Budeme teda vo výsledku vidieť, aký je rozdiel medzi zistenými početnosťami (Count) a očakávanými početnosťami (Expected). Môžeme zvoliť aj zobrazenie percent pod „Percentages“. „Row“ pre riadkové percentá a „Column“ pre stĺpcové percentá kontingenčnej tabuľky.

Výsledok:
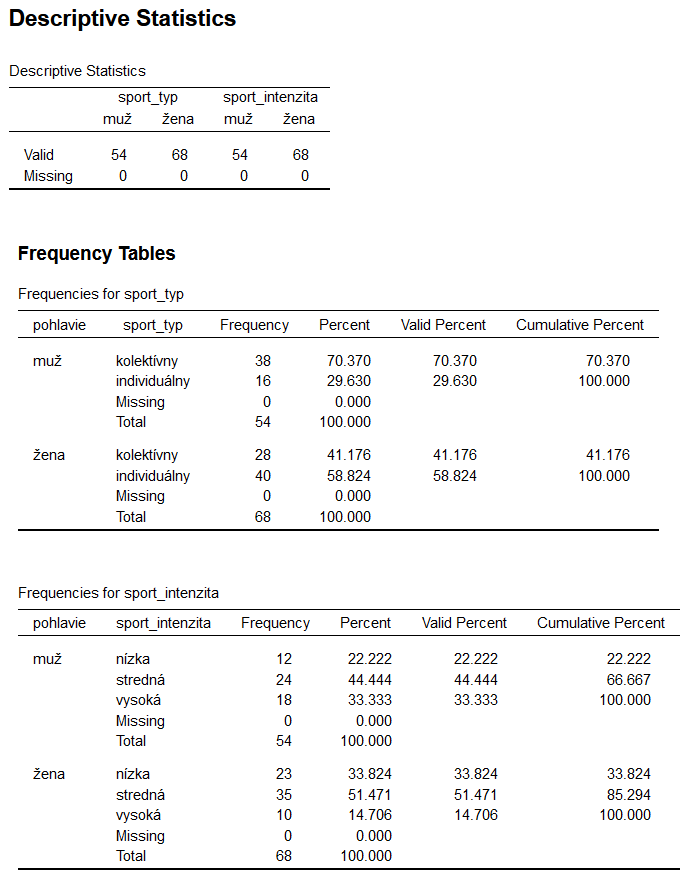
Pod týmto textom nájdete niekoľko tabuliek. Tabuľka s názvom „Descriptive Statistics“ zobrazuje vyššie zvolené hodnoty popisnej štatistiky. Zvolili sme si len zobrazenie „Valid“ (platných) a „Missing“ (chýbajúcich) hodnôt. Môžeme vidieť, že všetky hodnoty sú platné pre mužov aj ženy v premenných sport_typ a sport_intenzita. Ak by v niektorej z buniek dátovej tabuľky nebola číselná hodnota ale zostala by prázdna, videli by sme, že hodnota „Missing“ by mala inú ako nulovú hodnotu.
Ďalšie tabuľky pod týmto textom sú „Freqency Tables“, teda frekvenčné tabuľky s počtami hodnôt a percent pre jednotlivé premenné. Vrchná tabuľka je „Frequencies form sport_typ“ – teda počty pre typ športovej aktivity u mužov a žien, ktoré majú dve kategórie – kolektívny a individuálny. Popíšme si prvú tabuľku. Môžeme z nej vyčítať, že mužov, ktorí sa venujú kolektívnemu športu je 38 (Frekvency = počet/početnosť), či je 70,370% z celkového počtu mužov. Mužov, ktorí sa venujú individuálnemu športu je 16, čo tvorí 29,630% z celkového počtu mužov. Žien, ktoré sa venujú kolektívnemu športu je vo výskumnom súbore 28, čo tvorí 41,176% počtu žien a individuálnemu športu sa venuje 40 žien, čo je 58,824%. Obdobne by sme vedeli popísať aj tabuľku nižšie „Frequencies form sport_intenzita“. Stĺpec „Valid Percent“ nám hovorí o percente platných údajov. V našom prípade je toto číslo rovnaké ako v stĺpci „Percent“. Ak by sme mali ale v dátovom súbore chýbajúce hodnoty (Missing), hodnota „Valid Percent“ by sa od hodnoty „Percent“ líšila. Posledný stĺpec „Cumulative percent“ je súčet percentuálnych hodnôt predchádzajúcich kategórií. V tabuľke „Frequencies form sport_typ“ môžeme pomocou „Cumulative percent“ napr. vidieť, že mužov, ktorých intenzita športovania je nízka a stredná je 66,667%. Ženy s nízkou a strednou intenzitou športovania tvoria 85,294% všetkých žien.
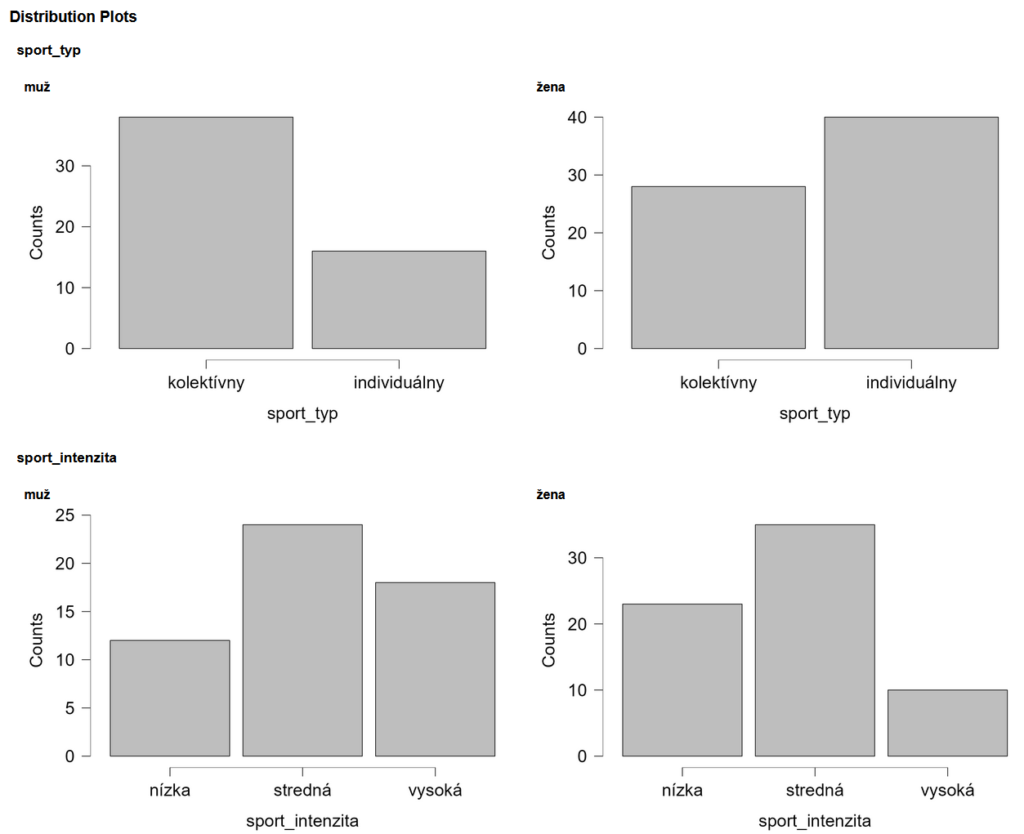
Pod týmto textom nájdeme stĺpcové grafy premennej sport_typ a pod nimi premennej sport_intenzita rozdelené podľa pohlavia. V analýze sme si ich volili v menu „Basic plots“.
Pod týmto textom nájdeme koláčové grafy (Pie Charts) premennej sport_typ a pod nimi premennej sport_intenzita rozdelené podľa pohlavia. V analýze sme si ich volili tiež v menu „Basic plots“.

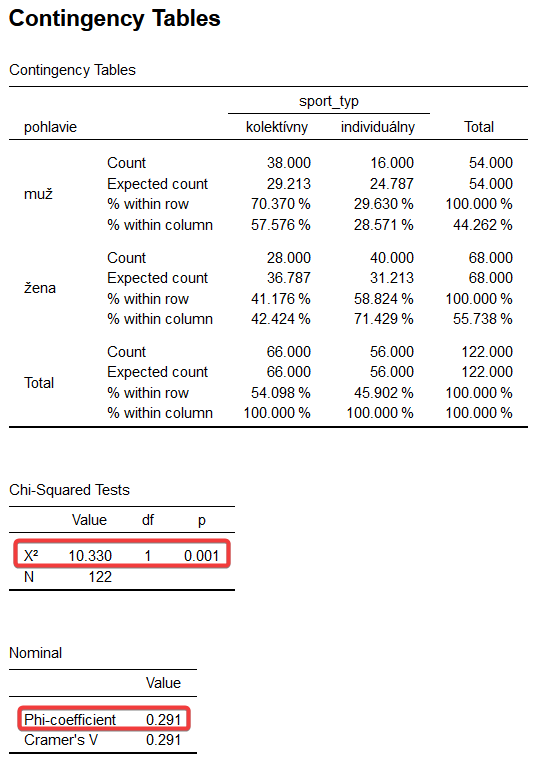
Pod týmto textom môžeme vidieť „Contingency Tables“ – kontingenčné/krížové tabuľky pre premenné sport_typ a pohlavie a pre premenné sport_intenzita a pohlavie. Opäť si môžeme prvú z nich popísať. Vidíme, že 38 mužov (57,576% venujúcich sa kolektívnemu športu) sa venuje kolektívnemu športu, pričom očakávaná (Expected count) hodnota je 29,213. Vidíme, že v našej výskumnej vzorke sme zistili o takmer 9 mužov viac venujúcich sa kolektívnemu športu, ako by bolo očakávané. Ak pokračujeme v interpretácii kolektívneho športu, vidíme že v našej výskumnej vzorke sa 28 žien (42,424% venujúcich sa kolektívnemu športu) venuje kolektívnemu športu. Očakávaný počet je v tomto prípade 36,787. V našej vzorke sa teda nachádza o takmer 9 žien venujúcich sa kolektívnemu športu menej ako by sme očakávali. Podobne interpretujeme individuálne športy. Vidíme, že 16 mužov (28,571% venujúcich sa individuálnemu športu) sa venuje individuálnemu športu, čo je o viac ako 8 menej, ako je hodnota očakávanej početnosti 24,787. Žien, venujúcich sa individuálnemu športu je vo výskumnej vzorke 40 (71,429% venujúcich sa individuálnemu športu), čo je o takmer 9 viac, ako je očakávaná početnosť 31,213. Vidíme teda, že očakávané početnosti sa od nami zistených líšia vo všetkých bunkách tabuľky.
Ďalšou tabuľkou, pod týmto textom je „Chi – Square Tests“ – tabuľka s hodnotou Chí-kvadrát (χ2) test nezávislosti, ktorý hovorí o tom, či existuje asociácia medzi analyzovanými nominálnymi premennými, v našom príklade medzi pohlavím (muž, žena) a typom športovej aktivity (kolektívny, individuálny). Pre rozhodnutie o tom, či asociácia medzi premennými existuje alebo nie slúži hodnota p, teda signifikancie. V našom prípade je p = 0,001. Je teda nižšie ako zvyčajne stanovená úroveň signifikancie 0,05. Prijímame záver (alternatívnu hypotézu) o tom, že existuje asociácia medzi analyzovanými nominálnymi premennými pohlavie a typ športu. Ak by hodnota p bola vyššia ako 0,05, záver by znel opačne, teda neexistuje asociácia medzi analyzovanými premennými.
Ďalšou tabuľkou s názvom „Nominal“ je výsledok výpočtu koeficientu phi a Cramerovho V. Ako je vyššie uvedené, pri analýze dvoch binárnych premenných, ako je to v tomto prípade pohlavie a typ športovej aktivity, kde vzniká kontingenčná tabuľka 2×2 interpretujeme koeficient phi. Cramerovo V v tomto prípade nadobúda rovnakú hodnotu ako phi ale neinterpretujeme ho. Koeficient phi podobne ako Cramerovo V interpretujeme v troch úrovniach, hladinách ako: nízky od 0 do 0,29; stredný do 0,30 do 0,49 a veľký viac ako 0,50 (Cohen, 1988). V našom prípade je sila asociácie medzi pohlavím a typom športovej aktivity vyjadrená koeficientom phi rovná 0,291, čo predstavuje nízku mieru asociácie.
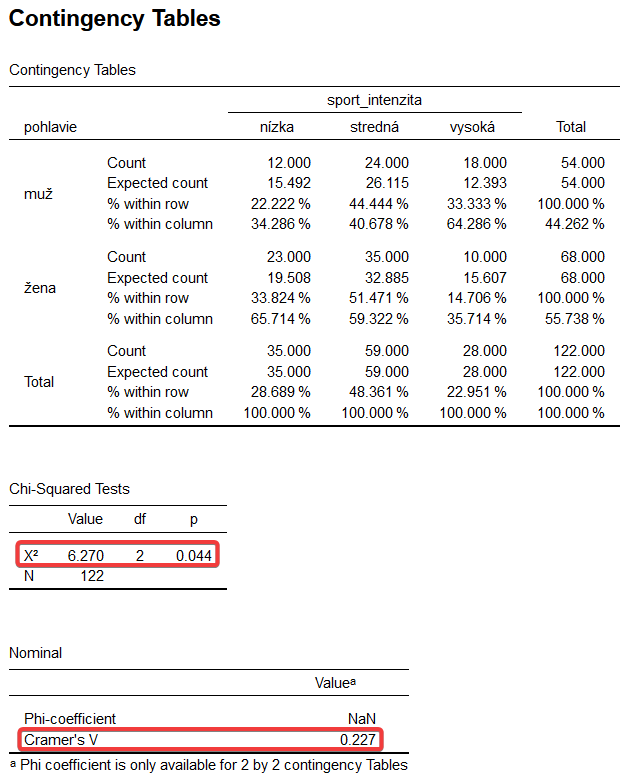
Pod týmto textom je opäť „Contingency Tables“ – kontingenčná/krížová tabuľka pre premenné sport_intenzita a pohlavie. Popísať ju možno podobne, ako je uvedené vyššie.
Ďalšou tabuľkou, pod týmto textom je „Chi – Square Tests“ – tabuľka s hodnotou Chí-kvadrát (χ2) test nezávislosti, ktorý hovorí o tom, či existuje asociácia medzi analyzovanými nominálnymi premennými, v našom príklade medzi pohlavím (muž, žena) a intenzita športovej aktivity (nízka, stredná, vysoká). Pre rozhodnutie o tom, či asociácia medzi premennými existuje alebo nie slúži hodnota p, teda signifikancie. V našom prípade je p = 0,044. Je teda nižšie ako zvyčajne stanovená úroveň signifikancie 0,05. Prijímame záver (alternatívnu hypotézu) o tom, že existuje asociácia medzi analyzovanými nominálnymi premennými pohlavie a intenzitou športu. Ak by hodnota p bola vyššia ako 0,05, záver by znel opačne, teda neexistuje asociácia medzi analyzovanými premennými.
Ďalšou tabuľkou s názvom „Nominal“ je výsledok výpočtu koeficientu phi – kde je uvedená hodnota NaN, pretože koeficient phi sa v tabuľke väčšej ako 2×2 nedá vypočítať. Tu nás zaujíma hodnota Cramerovho V, ktorá hovorí o sile asociácie mezdi premennou pohlavie a premennou intenzita športovej aktivity. Dosahuje hodnotu 0,227 a interpretujeme ju podľa hladín podobne, ako koeficient phi: nízky od 0 do 0,29; stredný do 0,30 do 0,49 a veľký viac ako 0,50 (Cohen, 1988). V našom prípade je sila asociácie medzi pohlavím a intenzitou športovej aktivity vyjadrená Cramerovým V rovná 0,227, čo predstavuje nízku mieru asociácie.
Ako výsledok zapísať:
VO1: Existuje asociácia medzi pohlavím a typom športovej aktivity – individuálnej, či kolektívnej?
Realizovali sme test Pearonovho χ2, aby sme zistili, či existuje asociácia medzi pohlavím a typom športovej aktivity – individuálnej, či kolektívnej. Všetky očakávané početnosti vo kontingenčnej tabuľke boli vyššie ako päť. Medzi pohlavím a výberom typu športovej aktivity existuje štatisticky významná asociácia χ 2 (1) = 10,330, p = 0,001, pričom mieru tejto asociácie môžeme hodnotiť ako slabú φ = 0,291.
VO2: Existuje asociácia medzi pohlavím a intenzitou športovej aktivity – nízkou, strednou, vysokou?
Realizovali sme test Pearonovho χ2, aby sme zistili, či existuje asociácia medzi pohlavím a intenzitou športovej aktivity – nízkou, strednou, vysokou. Všetky očakávané početnosti vo kontingenčnej tabuľke boli vyššie ako päť. Medzi pohlavím a intenzitou športovej aktivity existuje štatisticky významná asociácia χ 2 (1) = 6,270, p = 0,044, pričom mieru tejto asociácie môžeme hodnotiť ako slabú V = 0,227.
Použitá literatúra:
Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences (2nd Edition) (2nd ed.). Routledge.
Hanák, R. (2016). Dátová analýza pre sociálne vedy. Vydavateľstvo Ekonóm.
JASP. (n.d.). Study with us. University of Greenwich. https://gala.gre.ac.uk/id/eprint/25585/
Rabušic, L., Soukup, P., & Mareš, P. (2019). Statistická analýza sociálněvědních dat (prostřednictvím SPSS). Masarykova univerzita.
SPSS Statistics Tutorials and Statistical Guides | Laerd Statistics. (n.d.). https://statistics.laerd.com/
